Famous mathematicians | Mathematics Centre

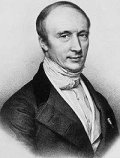
Augustin-Louis Cauchy (1789-1857, France) was extraordinarily prodigious, prolific and inventive. Home-schooled, he awed famous mathematicians at an early age. In contrast to Gauss and Newton, he was almost over-eager to publish; in his day his fame surpassed that of Gauss and has continued to grow. Cauchy did important work in analysis, algebra and number theory. One of his important contributions was the "theory of substitutions" (permutation group theory). Cauchy's research also included convergence of infinite series, differential equations, determinants, and probability. He invented the calculus of residues. Although he was one of the first great mathematicians to focus on abstract mathematics (another was Euler), he also made important contributions to mathematical physics, e.g. the theory of elasticity. He was the first to prove Fermat's conjecture that every positive integer can be expressed as the sum of k k-gon numbers for any k, and also refined Euler's results in discrete topology. Another of Cauchy's contributions was his insistence on rigorous proofs.

One of the duties of a great mathematician is to nurture his successors, but Cauchy selfishly dropped the ball on both of the two greatest young mathematicians of his day, mislaying the key manuscripts of both Abel and Galois. (For this historical miscontribution perhaps Cauchy should be demoted slightly.)

Source: Wikipedia

Leonardo Fibonacci was born in Pisa, Italy in about 1170. His father Guglielmo was nicknamed Bonaccio ("good natured" or "simple"). Leonardo's mother, Alessandra, died when he was nine years old. Leonardo was posthumously given the nickname Fibonacci (derived from filius Bonacci, meaning son of Bonaccio). Guglielmo directed a trading post (by some accounts he was the consultant for Pisa) in Bugia, a port east of Algiers in the Almohad dynasty's sultanate in North Africa (now Bejaia, Algeria). As a young boy, Leonardo traveled there to help him. This is where he learned about the Hindu-Arabic numeral system. Recognizing that arithmetic with Hindu-Arabic numerals is simpler and more efficient than with Roman numerals, Fibonacci traveled throughout the Mediterranean world to study under the leading Arab mathematicians of the time. Leonardo returned from his travels around 1200. In 1202, at age 32, he published what he had learned in Liber Abaci (Book of Abacus or Book of Calculation), and thereby introduced Hindu-Arabic numerals to Europe. Leonardo became an amicable guest of the Emperor Frederick II, who enjoyed mathematics and science. In 1240 the Republic of Pisa honored Leonardo, referred to as Leonardo Bigollo, by granting him a salary. In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers, starting with 0 and 1. Thus the sequence begins 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 etc... The higher up in the sequence, the closer two consecutive "Fibonacci numbers" of the sequence divided by each other will approach the golden ratio (approximately 1 : 1.618 or 0.618 : 1). The golden ratio was used widely in the Renaissance in paintings.

Q: What does a cafeteria lunch have in common with the Fibonacci sequence?

A: Each next lunch is the sum of two previous ones

The Fibonacci spiral is created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling - the one on the right uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34:

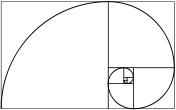
Source: Wikipedia

Baron (Jean Baptiste) Joseph Fourier (pronounced: Fooryay) (1768-1830) was born in Auxerre, France. He is considered the most famous French mathematician and physicist. He was the son of a tailor and born into a prominent family. Although initially trained for the priesthood, he turned to mathematics and became a teacher by the age of 16. Fourier was professor between 1795 and 1798) at the Ecole Polytechnique in Paris. He accompanied Napoleon I to Egypt and in 1808 he was made a baron. He died in Paris in 1830, Fourier never married.

Contributions:

Fourier had a very distinguised career and is famous for showing how the conduction of heat in solid bodies could be analyzed in terms of infinite mathematical series which is called the 'Fourier Series'. Fourier was the first correct theory on heat diffusion. His scientific writings are contained in two volumes. Published in 1822, the Fourier Series shows how a mathematical series of sine and cosine terms can be used to analyze heat conduction in solid bodies.

Fourier came upon his idea in connection with the problem of the flow of heat in solid bodies, including the earth. The formula x/2 = sin x - (sin 2x)/2 + (sin 3x)/3 + ... was published by Leonhard Euler (1707-1783) before Fourier's work began, so you might like to ponder the question why Euler did not receive the credit for Fourier's series.

Famous Works

Oeuvres de Fourier, 2 vol. (1888-90)
Analyse des equations determinees (1831)
Theorie analytique de la chaleur (1822 - The Analytical Theory of Heat, 1878, reprinted 1955)
Description de l'Egypte, 21 vol. (1808-25)

Famous Quote

"The profound study of nature is the most fertile source of mathematical discoveries."

Source: Wikipedia

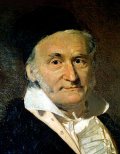
Johann Carl Friedrich Gauss (30 April 1777 - 23 February 1855), the "Prince of Mathematics," exhibited his calculative powers when he corrected his father's arithmetic before the age of three. His revolutionary nature was demonstrated at age twelve, when he began questioning the axioms of Euclid. His genius was confirmed at the age of nineteen when he proved that the regular n-gon was constructible, for odd n, if and only if n is the product of distinct prime Fermat numbers. At age 24 he published Disquisitiones Arithmeticae, probably the greatest book of pure mathematics ever.

Gauss built the theory of complex numbers into its modern form, including the notion of "monogenic" functions which are now ubiquitous in mathematical physics. The other contributions of Gauss are quite numerous and include the Fundamental Theorem of Algebra (that an n-th degree polynomial has n complex roots), hypergeometric series, foundations of statistics, and differential geometry. Gauss was the premier number theoretician of all time, proving Euler's Law of Quadratic Reciprocity. He also did important work in geometry, providing an improved solution to Apollonius' famous problem of tangent circles; stating and proving the Fundamental Theorem of Normal Axonometry, and solving astronomical problems related to comet orbits and navigation by the stars. Gauss also did important work in several areas of physics, and invented the heliotrope.

Much of Gauss's work wasn't published: unbeknownst to his colleagues it was Gauss who first discovered doubly periodic elliptic functions, non-Euclidean geometry, a prime distribution formula, quaternions, foundations of topology, the Law of Least Squares, Dirichlet's class number formula, the butterfly procedure for rapid calculation of Fourier series, and even the rudiments of knot theory. Also in this category is the Fundamental Theorem of Functions of a Complex Variable (that the line-integral over a closed curve of a monogenic function is zero): he proved this first but let Cauchy take the credit. Gauss is widely agreed to be the most brilliant and productive mathematician who ever lived and many would rank him #1; however several of the others on the list had more historical importance. Abel hints at a reason for this: "[Gauss] is like the fox, who effaces his tracks in the sand."

Gauss once wrote "It is not knowledge, but the act of learning, ... which grants the greatest enjoyment. When I have clarified and exhausted a subject, then I turn away from it, in order to go into darkness again ..."

Gauss was an ardent perfectionist and a hard worker. According to Isaac Asimov, Gauss was once interrupted in the middle of a problem and told that his wife was dying. He is purported to have said, "Tell her to wait a moment till I'm done." This anecdote is briefly discussed in G. Waldo Dunnington's Gauss, Titan of Science where it is suggested that it is an apocryphal story.

Source: Wikipedia

Pierre-Simon, marquis de Laplace (23 March 1749 - 5 March 1827) was a French mathematician and astronomer and is often called the "French Newton." His masterpiece was Mecanique Celeste which redeveloped and improved Newton's work on planetary motions using calculus. While Newton had shown that the two-body gravitation problem led to orbits which were ellipses (or other conic sections), Laplace was more interested in the much more difficult problems involving three or more bodies. (Would Jupiter's pull on Saturn eventually propel Saturn into a closer orbit, or was Saturn's orbit stable for eternity?) Laplace's equations had the optimistic outcome that the solar system was stable.

Laplace advanced the nebular hypothesis of solar system origin, and was first to conceive of black holes and multiple galaxies. He explained the so-called secular acceleration of the Moon. (Today we know Laplace's theories do not fully explain the Moon's path, nor guarantee orbit stability.) His other accomplishments in physics include theories about the speed of sound and surface tension. He was noted for his strong belief in determinism, famously replying to Napoleon's question about God with: "I have no need of that hypothesis.

Laplace viewed mathematics as just a tool for developing his physical theories. Nevertheless, he made many important mathematical discoveries and inventions, most notably the Laplace Transform. He was the premier expert at differential and difference equations, and definite integrals. He developed spherical harmonics, potential theory, the theory of determinants, and advanced Euler's technique of generating functions. In the fields of probability and statistics he made important advances: he proved the Law of Least Squares, and introduced the controversial ("Bayesian") rule of succession. In the theory of equations, he was first to prove that any polynomial of even degree must have a real quadratic factor.

Others might place Laplace higher on the list, but he proved no fundamental theorems of pure mathematics (though his partial differential equation for fluid dynamics is one of the most famous in physics), founded no major branch of pure mathematics, and wasn't particularly concerned with rigorous proof. (He is famous for skipping difficult proof steps with the phrase "It is easy to see".) Nevertheless he was surely one of the greatest applied mathematicians ever.

Source: Wikipedia

Joseph Louis Lagrange lived from 1736 to 1813 which is considered to be the beginnings of modern math. He was the oldest of 11 children and one of 2 who survived to adulthood. He was born in Italy (Turin, Sardinia-Piedmont ) but is considered to be the Italian born French mathematician. His interest in math started when he was a child and for the most part, he was a self-taught mathematician. By the age of 19, Lagrange was appointed professor of mathematics at the Royal Artillery School in Turin - after Euler stated how impressed he was with Lagrange's work on the tautochrone demonstrating his method of maxima and minima titled 'Calculus of Variation'.

His discoveries were important to the not yet named subject of 'Calculus'. He received 2 offers to work at the prestigious Berlin Academy and finally accepted the offer and succeeded Euler as the Director of Mathematics on November 6th, 1766 but then moved on to the Paris Academy of Science where he remained for the rest of his career.

Famous Quotes:

Before we take to sea we walk on land, before we create we must understand. When we ask advice, we are usually looking for an accomplice.

Contributions and publications:

• while in Prussia, he published the 'Mécanique Analytique' which is considered to be his monumental work in the pure maths.
• his most prominent influence was his contribution to the metric system and his addition of a decimal base, which is in place largely due to his plan. Some refer to Lagrange as the founder of the metric system.
• Lagrange is also known for a great deal of work on planetary motion. He was responsible for developing the groundwork for an alternate method of writing Newton's Equations of Motion. This is referred to as 'Lagrangian Mechanics'. In 1772, he described the Langrangian points, the points in the plane of two objects in orbit around their common center of gravity at which the combined gravitational forces are zero, and where a third particle of negligible mass can remain at rest. This is why Lagrange is referred to as an astronomer/mathematician.
• the Lagrangian polynomial is the far easiest way to find a curve through points.

Source: Wikipedia

Abraham de Moivre, (a good friend of Issac Newton) was born on May 16th 1667 in Vitry (close to Paris), France and died November 27th 1754 in London, England. Although De Moivre attended college and studied privately, it doesn't appear that he received a degree. He apparently served time in prison for about a year for being protestant. After serving his term and with the expulsion of the Huguenots, he emingrated to England. During his late teens, he worked as a private math tutor. In 1697 he was elected a fellow of the Royal Society. By 1710 he was appointed to the Commission set up by the Royal Society to review the claims of Newton and Leibniz who eventually discovered calculus. de Moivre was a foreigner which makes it difficult to gain an appointment with the Commission, however, due to his friendship with Newton, he was appointed. De Moivre's main income came from tutoring and it's believe that he lived in poverty for his entire life.

Contributions:

• de Moivre pioneered the analytic trigonometry/geometry and the theory of probability.
• he is famous for De Moivre's Formula - a fundamental formula on complex numbers.
• during his studies in probability, he also developed the foundations in the theory of annuities.
• he published The Doctrine of Chance in 1718.

Source: Wikipedia

Pierre de Fermat was born in Beaumont-de-Lomagne, France in August of 1601 and died in 1665. He is considered to be one of the greatest mathematicians of the seventeenth century. Fermat's father was a leather merchant and his mother's family was in the legal profession. Fermat attended a Franciscan monastery before moving on to obtain a Bachelor's Degree in civil law from the University of Orleans in 1631. He married, had five children and practiced law.